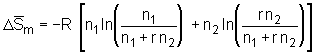 , (5.1)
wobei R die Gaskonstante ist und n1 bzw. n2 der Stoffmenge des Lösemittels bzw. des Polymeren entsprechen. r ist der Polymerisationsgrad der Komponente 2, das heißt die Zahl der sich wiederholenden Monomereinheiten der Polymerkomponente.
In den Berechnungen der Mischungsentropie
, (5.1)
wobei R die Gaskonstante ist und n1 bzw. n2 der Stoffmenge des Lösemittels bzw. des Polymeren entsprechen. r ist der Polymerisationsgrad der Komponente 2, das heißt die Zahl der sich wiederholenden Monomereinheiten der Polymerkomponente.
In den Berechnungen der Mischungsentropie 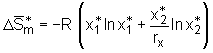 . (5.4)
Für die dargestellte Herleitung gilt unter anderen die Voraussetzung, daß es sich um ein athermisches System handelt, das heißt
. (5.4)
Für die dargestellte Herleitung gilt unter anderen die Voraussetzung, daß es sich um ein athermisches System handelt, das heißt 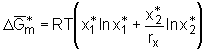 . (5.6b)
Die Änderung des chemischen Potentials des Lösemittels D
m
1, hervorgerufen durch den Mischungsprozeß eines Polymers mit einem Lösemittel, ist durch den Differentialquotienten
. (5.6b)
Die Änderung des chemischen Potentials des Lösemittels D
m
1, hervorgerufen durch den Mischungsprozeß eines Polymers mit einem Lösemittel, ist durch den Differentialquotienten
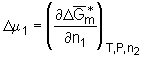 (5.7a)
bzw. mit Gl.(5.6a) durch
(5.7a)
bzw. mit Gl.(5.6a) durch
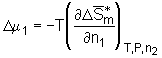 (5.7b)
bestimmt. Hierbei werden die Temperatur T, der Druck P und die Stoffmenge des Polymers n2 konstant gehalten. Anwendung der Gl.(5.7a) auf Gl.(5.6b) führt zu
(5.7b)
bestimmt. Hierbei werden die Temperatur T, der Druck P und die Stoffmenge des Polymers n2 konstant gehalten. Anwendung der Gl.(5.7a) auf Gl.(5.6b) führt zu
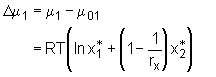 , (5.8)
mit m
1 dem chemischen Potential des Lösemittels in der Lösung und m
01 dem chemischen Potential des reinen Lösemittels.
, (5.8)
mit m
1 dem chemischen Potential des Lösemittels in der Lösung und m
01 dem chemischen Potential des reinen Lösemittels.
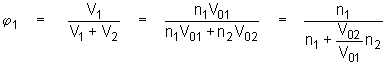 (5.9a)
mit
(5.9a)
mit 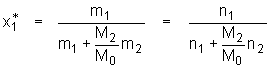 (5.10a)
mit
(5.10a)
mit 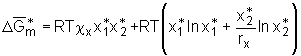 . (5.13)
Für die Änderung des chemischen Potentials des Lösemittels ergibt sich hieraus durch Bildung des Differentialquotienten
. (5.13)
Für die Änderung des chemischen Potentials des Lösemittels ergibt sich hieraus durch Bildung des Differentialquotienten 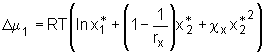 . (5.14)
. (5.14)
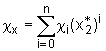 . (5.15)
Für i=0 ist kein konzentrationsabhängiger Term in dieser Reihenentwicklung berücksichtigt. Die Größen c
i in Gl.(5.15) sind nur von Temperatur und Druck abhängig.
Betrachtet man nur die Temperaturabhängigkeit des Wechselwirkungsparameters, wird diese allgemein ebenfalls durch eine Reihenentwicklung wiedergegeben [76].
. (5.15)
Für i=0 ist kein konzentrationsabhängiger Term in dieser Reihenentwicklung berücksichtigt. Die Größen c
i in Gl.(5.15) sind nur von Temperatur und Druck abhängig.
Betrachtet man nur die Temperaturabhängigkeit des Wechselwirkungsparameters, wird diese allgemein ebenfalls durch eine Reihenentwicklung wiedergegeben [76].
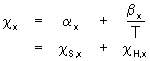 (5.17)
a
x ist hier der entropische Anteil, während b
x den enthalpischen Anteil des Wechselwirkungsparameters wiedergibt, der der sogenannten Überschußwechselwirkungsenergie proportional ist.
(5.17)
a
x ist hier der entropische Anteil, während b
x den enthalpischen Anteil des Wechselwirkungsparameters wiedergibt, der der sogenannten Überschußwechselwirkungsenergie proportional ist.
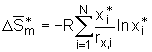 (5.18)
bzw. für die Mischungsenthalpie
(5.18)
bzw. für die Mischungsenthalpie
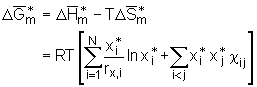 mit j=2,3, ... . (5.20)
Betrachtet man nun zum Beispiel ein 3-Komponentensystem wird aus Gl.(5.20)
mit j=2,3, ... . (5.20)
Betrachtet man nun zum Beispiel ein 3-Komponentensystem wird aus Gl.(5.20)
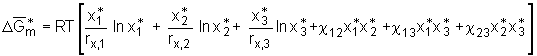 . (5.21)
Partielles Ableiten dieses Ausdrucks nach n1 unter Konstanthaltung der Temperatur, des Drucks und der Stoffmengen n2 und n3, führt, analog zu der Herleitung für ein binäres System, zum chemischen Potential
. (5.21)
Partielles Ableiten dieses Ausdrucks nach n1 unter Konstanthaltung der Temperatur, des Drucks und der Stoffmengen n2 und n3, führt, analog zu der Herleitung für ein binäres System, zum chemischen Potential 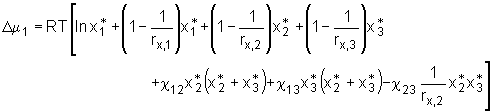 (5.22)
(5.22)
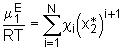 , (5.24)
und der Bedingung
, (5.24)
und der Bedingung 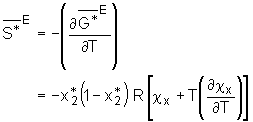 (5.26)
mit der Freien Exzeßenthalpie verbunden. Für die Exzeßenthalpie
(5.26)
mit der Freien Exzeßenthalpie verbunden. Für die Exzeßenthalpie 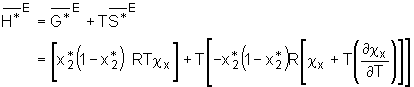 . (5.27)
Entsprechend der Gleichungen der Exzeßentropie bzw. -enthalpie für binäre Systeme können die Terme für Mehrkomponentensysteme hergeleitet werden. Betrachtet man z. B. die Exzeßgrößen für ternäre Systeme, lautet die freie Exzeßenthalpie
. (5.27)
Entsprechend der Gleichungen der Exzeßentropie bzw. -enthalpie für binäre Systeme können die Terme für Mehrkomponentensysteme hergeleitet werden. Betrachtet man z. B. die Exzeßgrößen für ternäre Systeme, lautet die freie Exzeßenthalpie
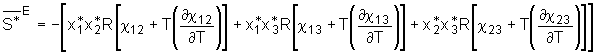 (5.29)
Analog Gl.(5.27) folgt somit für die Exzeßenthalpie
(5.29)
Analog Gl.(5.27) folgt somit für die Exzeßenthalpie
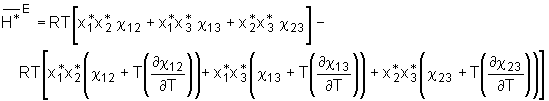
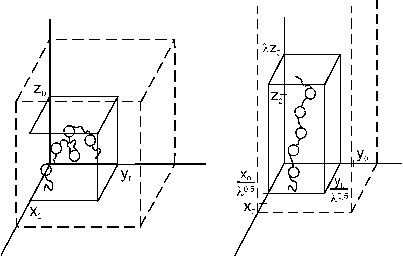 Abb.(5.1): Darstellung der uniaxialen Dehnung einer Probe in z-Richtung. Hierbei kennzeichnen die durchgezogenen Linien das betrachtete Volumenelement; die gestrichelten Linien veranschaulichen die Gesamtprobe [68].
Die Änderung der Entropie eines Netzbogens, die durch eine solche affine Deformation der Probe verursacht wird, ist über die Boltzmann-Gleichung mit der thermodynamischen Wahrscheinlichkeit verknüpft. Die Gesamtentropieänderung des Netzwerks
Abb.(5.1): Darstellung der uniaxialen Dehnung einer Probe in z-Richtung. Hierbei kennzeichnen die durchgezogenen Linien das betrachtete Volumenelement; die gestrichelten Linien veranschaulichen die Gesamtprobe [68].
Die Änderung der Entropie eines Netzbogens, die durch eine solche affine Deformation der Probe verursacht wird, ist über die Boltzmann-Gleichung mit der thermodynamischen Wahrscheinlichkeit verknüpft. Die Gesamtentropieänderung des Netzwerks 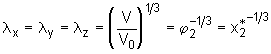 (5.34)
V ist das Volumen der gequollenen Gelmischphase bzw. V0 das Volumen des isotropen, ungequollenen Netzwerks. Ersetzen der relativen Längenverhältnisse l
i in Gl.(5.62) führt, unter Benutzung des Grundmolenbruchs, zu dem Zusammenhang
(5.34)
V ist das Volumen der gequollenen Gelmischphase bzw. V0 das Volumen des isotropen, ungequollenen Netzwerks. Ersetzen der relativen Längenverhältnisse l
i in Gl.(5.62) führt, unter Benutzung des Grundmolenbruchs, zu dem Zusammenhang
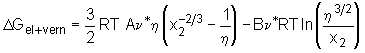 . (5.35)
Die Größe A wird als "Strukturfaktor" bezeichnet, der die Mikrostruktur des Netzwerks berücksichtigt. B ist der sogenannte "Volumenfaktor". Zuerst von Tobolsky als "Memory Term" eingeführt, wird die Größe h
auch als Dilatationsfaktor bezeichnet [80].
. (5.35)
Die Größe A wird als "Strukturfaktor" bezeichnet, der die Mikrostruktur des Netzwerks berücksichtigt. B ist der sogenannte "Volumenfaktor". Zuerst von Tobolsky als "Memory Term" eingeführt, wird die Größe h
auch als Dilatationsfaktor bezeichnet [80].
| Autoren |
A |
B |
| James und Guth [61,62] |
0,5 |
0 |
| Flory und Rehner [50] Flory und Wall [66] |
1 |
0,5 |
| J. J. Hermans [65] |
1 |
1 |
| Duiser und Staverman [83] |
1-2/f |
0,5 |
| Eichinger [84] Graessley [85] Edwards [89] |
1-2/f |
0 |
| Ziabicky [90] |
1 |
0,5 |
| Flory [86,87] Phantom-Netzwerk reales Netzwerk |
1-2/f 1 |
0 2/f |
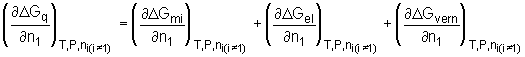 (5.38)
(5.38)
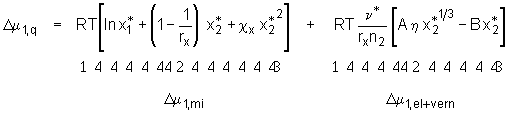 (5.39)
Die Größe
(5.39)
Die Größe 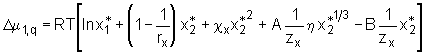 (5.40)
ergibt [78]. Im folgenden wird das Produkt
(5.40)
ergibt [78]. Im folgenden wird das Produkt 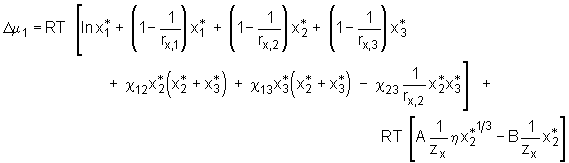 (5.41)
(5.41)
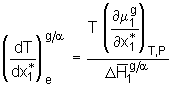 . (5.44)
Die Größe
. (5.44)
Die Größe 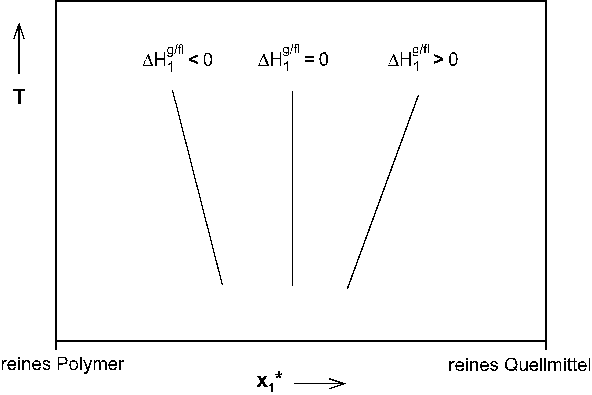 Abb.(5.2): Schematische Darstellung des Verlaufs einer Quellungskurve im Bereich des flüssigen Quellmittels unter Berücksichtigung des Einflusses der differentiellen Verdünnungsenthalpie auf das Vorzeichen der Steigung der Quellungskurve.
Abb.(5.2): Schematische Darstellung des Verlaufs einer Quellungskurve im Bereich des flüssigen Quellmittels unter Berücksichtigung des Einflusses der differentiellen Verdünnungsenthalpie auf das Vorzeichen der Steigung der Quellungskurve.
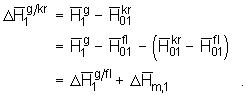 (5.46)
(5.46)
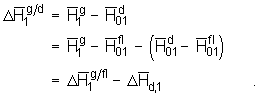 (5.47)
Durch diese einfache Transformation, das heißt Addition und direkte Subtraktion der molaren Enthalpie des reinen flüssigen Quellmittels, ergibt sich
(5.47)
Durch diese einfache Transformation, das heißt Addition und direkte Subtraktion der molaren Enthalpie des reinen flüssigen Quellmittels, ergibt sich 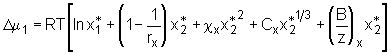 (5.49)
gegeben. Im heterogenen Gleichgewicht gilt
(5.49)
gegeben. Im heterogenen Gleichgewicht gilt 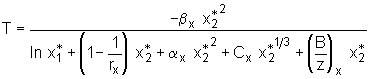 . (5.50)
In dieser Gleichung sind sowohl der Volumenterm
. (5.50)
In dieser Gleichung sind sowohl der Volumenterm 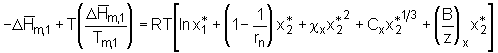 . (5.52)
In dieser Gleichung stehen zwei Größen, die eine Temperaturabhängigkeit aufweisen, die Schmelzenthalpie des Quellmittels und der FHSS-Wechselwirkungsparameter. Wird, wie in Gl.(5.50), der Ansatz
. (5.52)
In dieser Gleichung stehen zwei Größen, die eine Temperaturabhängigkeit aufweisen, die Schmelzenthalpie des Quellmittels und der FHSS-Wechselwirkungsparameter. Wird, wie in Gl.(5.50), der Ansatz 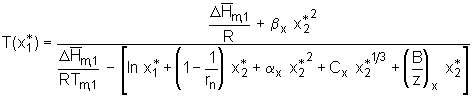 . (5.53)
In Analogie zu den Ausdrücken für die Beschreibung der Gele als binäre Systeme sind in dieser Arbeit Gleichungen abgeleitet worden, die die Gele als Drei-Komponenten-Systeme wiedergeben. Werden diese Ausdrücke für die Herleitung der T(
. (5.53)
In Analogie zu den Ausdrücken für die Beschreibung der Gele als binäre Systeme sind in dieser Arbeit Gleichungen abgeleitet worden, die die Gele als Drei-Komponenten-Systeme wiedergeben. Werden diese Ausdrücke für die Herleitung der T(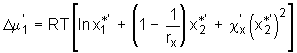 . (5.61)
. (5.61)
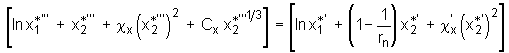 , (5.64)
wobei rx der Polymerisationsgrad des Polymers in der Lösung ist. Gl.(5.64) stellt eine zweite Bestimmungsgleichung für die Ermittlung der Größen Cx und
, (5.64)
wobei rx der Polymerisationsgrad des Polymers in der Lösung ist. Gl.(5.64) stellt eine zweite Bestimmungsgleichung für die Ermittlung der Größen Cx und 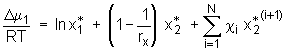 (5.65)
Der Index 1 kennzeichnet das Lösemittel, während der Index 2 die Polymerkomponente bezeichnet. Mit rx =
(5.65)
Der Index 1 kennzeichnet das Lösemittel, während der Index 2 die Polymerkomponente bezeichnet. Mit rx =  , (5.66a)
, (5.66a)
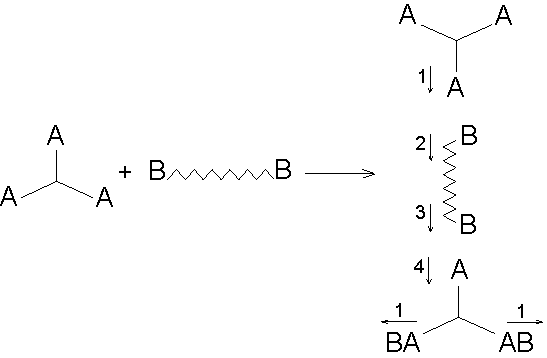 Abb.(5.3): Beispiel eines Reaktionsschemas einer Netzwerkbildungsreaktion, wobei die Komponente
Abb.(5.3): Beispiel eines Reaktionsschemas einer Netzwerkbildungsreaktion, wobei die Komponente 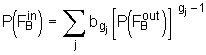 (5.71)
gegeben. In Analogie zu der Wahrscheinlichkeit
(5.71)
gegeben. In Analogie zu der Wahrscheinlichkeit 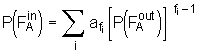 . (5.73)
pb bezeichnet hierbei den Anteil an Molekülen B, die reagiert haben. Die Kombination der Gl.(5.70) und (5.73) liefert den Zusammenhang
. (5.73)
pb bezeichnet hierbei den Anteil an Molekülen B, die reagiert haben. Die Kombination der Gl.(5.70) und (5.73) liefert den Zusammenhang
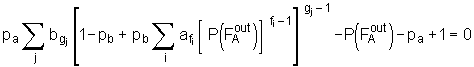 . (5.74)
Der Wert löslicher bzw. extrahierbarer Anteile, die nach abgeschlossener Netzwerkbildung im Netzwerk verbleiben, ist experimentell zugänglich. Ist ein Molekül A oder B Teil der löslichen Anteile ws muß jeder "Arm" eines solchen Moleküls zu einer endlichen Kette führen
. (5.74)
Der Wert löslicher bzw. extrahierbarer Anteile, die nach abgeschlossener Netzwerkbildung im Netzwerk verbleiben, ist experimentell zugänglich. Ist ein Molekül A oder B Teil der löslichen Anteile ws muß jeder "Arm" eines solchen Moleküls zu einer endlichen Kette führen
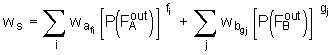 , (5.75)
wobei die Größen
, (5.75)
wobei die Größen 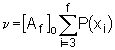 . (5.77)
Da eine elastisch aktive Kette an beiden Enden mit einem solchen Knotenpunkt verknüpft ist, folgt, daß die Zahl elastisch aktiver Ketten n
eff über den folgenden Zusammenhang berechnet werden kann
. (5.77)
Da eine elastisch aktive Kette an beiden Enden mit einem solchen Knotenpunkt verknüpft ist, folgt, daß die Zahl elastisch aktiver Ketten n
eff über den folgenden Zusammenhang berechnet werden kann
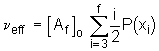 . (5.78)
. (5.78)